Recursion in C language

What is Recursion ?

        Function calling itself is called Recursion
Recursion is a programming technique that allows the programmer to express operations in terms of themselves. In C, this takes the form of a function that calls itself. A useful way to think of recursive functions is to imagine them as a process being performed where one of the instructions is to "repeat the process".

In the following example, recursion is used to calculate the factorial of a number.

1. #include <stdio.h>  
2. int fact (int);  
3. int main()  
4. {  
5.     int n,f;  
6.     printf("Enter the number whose factorial you want to calculate?");  
7.     scanf("%d",&n);  
8.     f = fact(n);  
9.     printf("factorial = %d",f);  
10. }  
11. int fact(int n)  
12. {  
13.     if (n==0)  
14.     {  
15.         return 0;  
16.     }  
17.     else if ( n == 1)  
18.     {  
19.         return 1;  
20.     }  
21.     else   
22.     {  
23.         return n*fact(n-1);  
24.     }  
25. }  

Output

Enter the number whose factorial you want to calculate?5
factorial = 120 

We can understand the above program of the recursive method call by the figure given below:

Recursive Function

A recursive function performs the tasks by dividing it into the subtasks. There is a termination condition defined in the function which is satisfied by some specific subtask. After this, the recursion stops and the final result is returned from the function.

The case at which the function doesn't recur is called the base case whereas the instances where the function keeps calling itself to perform a subtask, is called the recursive case. All the recursive functions can be written using this format.

Pseudocode for writing any recursive function is given below.

1. if (test_for_base)  
2. {  
3.     return some_value;  
4. }  
5. else if (test_for_another_base)  
6. {  
7.     return some_another_value;  
8. }  
9. else  
10. {  
11.     // Statements;  
12.     recursive call;  
13. }  

Example of recursion in C

Let's see an example to find the nth term of the Fibonacci series.

1. #include<stdio.h>  
2. int fibonacci(int);  
3. void main ()  
4. {  
5.     int n,f;  
6.     printf("Enter the value of n?");  
7.     scanf("%d",&n);  
8.     f = fibonacci(n);  
9.     printf("%d",f);  
10. }  
11. int fibonacci (int n)  
12. {  
13.     if (n==0)  
14.     {  
15.     return 0;  
16.     }  
17.     else if (n == 1)  
18.     {  
19.         return 1;   
20.     }  
21.     else  
22.     {  
23.         return fibonacci(n-1)+fibonacci(n-2);  
24.     }  
25. }  

Output

Enter the value of n?12 
144 

Memory allocation of Recursive method

Each recursive call creates a new copy of that method in the memory. Once some data is returned by the method, the copy is removed from the memory. Since all the variables and other stuff declared inside function get stored in the stack, therefore a separate stack is maintained at each recursive call. Once the value is returned from the corresponding function, the stack gets destroyed. Recursion involves so much complexity in resolving and tracking the values at each recursive call. Therefore we need to maintain the stack and track the values of the variables defined in the stack.

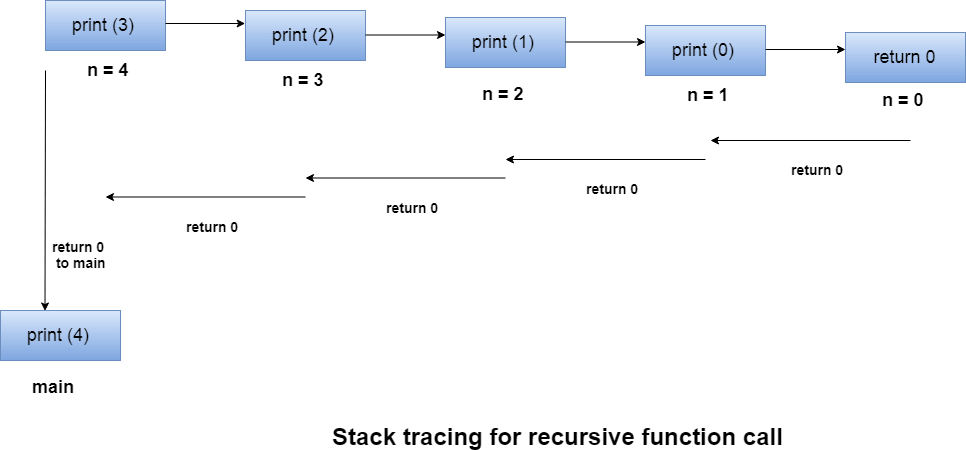
Let us consider the following example to understand the memory allocation of the recursive functions.

1. int display (int n)  
2. {  
3.     if(n == 0)  
4.         return 0; // terminating condition  
5.     else   
6.     {  
7.         printf("%d",n);  
8.         return display(n-1); // recursive call  
9.     }  
10. }  

Explanation

Let us examine this recursive function for n = 4. First, all the stacks are maintained which prints the corresponding value of n until n becomes 0, Once the termination condition is reached, the stacks get destroyed one by one by returning 0 to its calling stack. Consider the following image for more information regarding the stack trace for the recursive functions.

By Study For Future